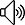引入特征函數是非常自然的事情:
接下來,Laplace 變換行不行?當然也可以,這其實是一碼事。統計物理學家很熟悉的「配分函數」也就是一個特征函數: ,它就對應于態密度 g(E) 的Laplace 變換。對物理學家而言,喜歡用逆溫度(Laplace),或者喜歡用虛時間(Fourier)這其實是一碼事的,如果在這種時候用虛時間來寫,一個好處是顯得高端大氣,另一個好處是可以與路徑積分聯系起來,而且,Laplace 變換用的時候總得要寫「正半軸」之類的東西,寫起來太麻煩。
,它就對應于態密度 g(E) 的Laplace 變換。對物理學家而言,喜歡用逆溫度(Laplace),或者喜歡用虛時間(Fourier)這其實是一碼事的,如果在這種時候用虛時間來寫,一個好處是顯得高端大氣,另一個好處是可以與路徑積分聯系起來,而且,Laplace 變換用的時候總得要寫「正半軸」之類的東西,寫起來太麻煩。
-
在實際應用中,逐個測量事件空間中的各事件發生的概率(或者分布函數)是極端困難的,相反,對大多數分布而言,矩(平均值、方差以及各種高階矩)往往是容易被測量的;
- 在問題變得復雜之后,再來計算矩(例如均值、方差等等)的時候,如果我們知道分布函數,那么我們要做的是求和與積分,而如果我們知道特征函數,在計算矩的時候,我們要做的只是微分,而通常,求導會比直接積分更容易,而且可以針對各階矩有更統一的形式。
接下來,Laplace 變換行不行?當然也可以,這其實是一碼事。統計物理學家很熟悉的「配分函數」也就是一個特征函數:
 ,它就對應于態密度 g(E) 的Laplace 變換。對物理學家而言,喜歡用逆溫度(Laplace),或者喜歡用虛時間(Fourier)這其實是一碼事的,如果在這種時候用虛時間來寫,一個好處是顯得高端大氣,另一個好處是可以與路徑積分聯系起來,而且,Laplace 變換用的時候總得要寫「正半軸」之類的東西,寫起來太麻煩。
,它就對應于態密度 g(E) 的Laplace 變換。對物理學家而言,喜歡用逆溫度(Laplace),或者喜歡用虛時間(Fourier)這其實是一碼事的,如果在這種時候用虛時間來寫,一個好處是顯得高端大氣,另一個好處是可以與路徑積分聯系起來,而且,Laplace 變換用的時候總得要寫「正半軸」之類的東西,寫起來太麻煩。
更多文章、技術交流、商務合作、聯系博主
微信掃碼或搜索:z360901061

微信掃一掃加我為好友
QQ號聯系: 360901061
您的支持是博主寫作最大的動力,如果您喜歡我的文章,感覺我的文章對您有幫助,請用微信掃描下面二維碼支持博主2元、5元、10元、20元等您想捐的金額吧,狠狠點擊下面給點支持吧,站長非常感激您!手機微信長按不能支付解決辦法:請將微信支付二維碼保存到相冊,切換到微信,然后點擊微信右上角掃一掃功能,選擇支付二維碼完成支付。
【本文對您有幫助就好】元