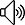（1）Lucas定理：p為素數(shù)，則有:
（2）證明：?n=(ak...a2,a1,a0)p = (ak...a2,a1)p*p + a0?=? [n/p]*p+a0，m=[m/p]*p+b0其次，我們知道，對任意質(zhì)數(shù)p有(1+x)^p=1+(x^p)(mod p) 。我們只要證明這個式子：C(n,m)=C([n/p],[m/p]) * C(a0,b0)(mod p)，那么就可以用歸納法證明整個定理。對于模p而言，我們有下面的式子成立：
上式左右兩邊的x的某項x^m(m<=n)的系數(shù)對模p同余。其中左邊的x^m的系數(shù)是 C(n,m)。 而由于a0和b0都小于p，因此右邊的x^m 一定是由 x^([m/p]*p) 和 x^b0 (即i=[m/p] , j=b0 )?相乘而得 因此有：C(n,m)=C([n/p],[m/p]) * C(a0,b0)? (mod p)。
（3）拓展應(yīng)用：上面的p是素數(shù)，那么不是素數(shù)怎么辦呢？若不是素數(shù)，將p分解質(zhì)因數(shù)，將C(n,m)分別按照（1）中的方法求對p的質(zhì)因數(shù)的模，然后用中國剩余定理合并。比如計算C(10,3)%14。C(10,3)=120,14有兩個質(zhì)因數(shù)2和7，120%2=0,120%7=1,這樣用(2,0)(7,1)找到最小的正整數(shù)8即是答案，即C(10,3)%14=8。注意，這里只適用于p分解完質(zhì)因數(shù)后每個質(zhì)因數(shù)只出現(xiàn)一次，例如12=2*2*3就不行，因為2出現(xiàn)了兩次。若p分解完質(zhì)因數(shù)后，含有某個質(zhì)因數(shù)出現(xiàn)多次，比如C(10,3)%98,其中98=2*7*7,此時就要把7*7看做一個數(shù),即:120%2=0,120%49=22,用(2,0)(49,22)和中國剩余定理得到答案22，即C(10,3)%98=22。此時，你又會有疑問，C(10,3)%49不也是模一個非素數(shù)嗎？此時不同的是這個非素數(shù)不是一般的非素數(shù)，而是某個素數(shù)的某次方。下面（4）介紹如何計算C(n,m)%p^t(t>=2,p為素數(shù))。
（4）計算C(n,m)%p^t。我們知道，C(n,m)=n!/m!/(n-m)!，若我們可以計算出n!%p^t，我們就能計算出m!%p^t以及(n-m)!%p^t。我們不妨設(shè)x=n!%p^t,y=m!%p^t,z=(n-m)!%p^t,那么答案就是x*reverse(y,p^t)*reverse(z,p^t)(reverse(a,b)計算a對b的乘法逆元)。那么下面問題就轉(zhuǎn)化成如何計算n!%p^t。比如p=3,t=2,n=19,
n!=1*2*3*4*5*6*7*8*?……*19
? ?=[1*2*4*5*7*8*… *16*17*19]*(3*6*9*12*15*18)
? ?=[1*2*4*5*7*8*… *16*17*19]*3^6(1*2*3*4*5*6)
然后發(fā)現(xiàn)后面的是(n/p)!，于是遞歸即可。前半部分是以p^t為周期的[1*2*4*5*7*8]=[10*11*13*14*16*17](mod 9)。下面是孤立的19，可以知道孤立出來的長度不超過 p^t,于是暴力即可。那么最后剩下的3^6啊這些數(shù)怎么辦呢？我們只要計算出n!,m!,(n-m)!里含有多少個p(不妨設(shè)a,b,c)，那么a-b-c就是C(n,m)中p的個數(shù)，直接算一下就行。
至此整個計算C(n,m)%p(p為任意數(shù))的問題完美解決。下面給出代碼：
?
i64 POW(i64 a,i64 b,i64 mod)
{
i64 ans=1;
while(b)
{
if(b&1) ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
i64 POW(i64 a,i64 b)
{
i64 ans=1;
while(b)
{
if(b&1) ans=ans*a;
a=a*a;
b>>=1;
}
return ans;
}
i64 exGcd(i64 a,i64 b,i64 &x,i64 &y)
{
i64 t,d;
if(!b)
{
x=1;
y=0;
return a;
}
d=exGcd(b,a%b,x,y);
t=x;
x=y;
y=t-a/b*y;
return d;
}
bool modular(i64 a[],i64 m[],i64 k)
{
i64 d,t,c,x,y,i;
for(i=2;i<=k;i++)
{
d=exGcd(m[1],m[i],x,y);
c=a[i]-a[1];
if(c%d) return false;
t=m[i]/d;
x=(c/d*x%t+t)%t;
a[1]=m[1]*x+a[1];
m[1]=m[1]*m[i]/d;
}
return true;
}
i64 reverse(i64 a,i64 b)
{
i64 x,y;
exGcd(a,b,x,y);
return (x%b+b)%b;
}
i64 C(i64 n,i64 m,i64 mod)
{
if(m>n) return 0;
i64 ans=1,i,a,b;
for(i=1;i<=m;i++)
{
a=(n+1-i)%mod;
b=reverse(i%mod,mod);
ans=ans*a%mod*b%mod;
}
return ans;
}
i64 C1(i64 n,i64 m,i64 mod)
{
if(m==0) return 1;
return C(n%mod,m%mod,mod)*C1(n/mod,m/mod,mod)%mod;
}
i64 cal(i64 n,i64 p,i64 t)
{
if(!n) return 1;
i64 x=POW(p,t),i,y=n/x,temp=1;
for(i=1;i<=x;i++) if(i%p) temp=temp*i%x;
i64 ans=POW(temp,y,x);
for(i=y*x+1;i<=n;i++) if(i%p) ans=ans*i%x;
return ans*cal(n/p,p,t)%x;
}
i64 C2(i64 n,i64 m,i64 p,i64 t)
{
i64 x=POW(p,t);
i64 a,b,c,ap=0,bp=0,cp=0,temp;
for(temp=n;temp;temp/=p) ap+=temp/p;
for(temp=m;temp;temp/=p) bp+=temp/p;
for(temp=n-m;temp;temp/=p) cp+=temp/p;
ap=ap-bp-cp;
i64 ans=POW(p,ap,x);
a=cal(n,p,t);
b=cal(m,p,t);
c=cal(n-m,p,t);
ans=ans*a%x*reverse(b,x)%x*reverse(c,x)%x;
return ans;
}
//計算C(n,m)%mod
i64 Lucas(i64 n,i64 m,i64 mod)
{
i64 i,t,cnt=0;
i64 A[205],M[205];
for(i=2;i*i<=mod;i++) if(mod%i==0)
{
t=0;
while(mod%i==0)
{
t++;
mod/=i;
}
M[++cnt]=POW(i,t);
if(t==1) A[cnt]=C1(n,m,i);
else A[cnt]=C2(n,m,i,t);
}
if(mod>1)
{
M[++cnt]=mod;
A[cnt]=C1(n,m,mod);
}
modular(A,M,cnt);
return A[1];
}
?
?
更多文章、技術(shù)交流、商務(wù)合作、聯(lián)系博主
微信掃碼或搜索：z360901061
微信掃一掃加我為好友
QQ號聯(lián)系： 360901061
您的支持是博主寫作最大的動力，如果您喜歡我的文章，感覺我的文章對您有幫助，請用微信掃描下面二維碼支持博主2元、5元、10元、20元等您想捐的金額吧，狠狠點擊下面給點支持吧，站長非常感激您！手機微信長按不能支付解決辦法：請將微信支付二維碼保存到相冊，切換到微信，然后點擊微信右上角掃一掃功能，選擇支付二維碼完成支付。
【本文對您有幫助就好】元
